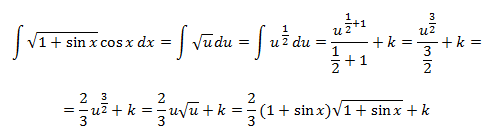INTEGRALES. POR PARTES.

EJERCICIOS DE INTEGRACIÓN POR PARTES. 

Cuando vemos que el integrando está formado por un producto, o por una división que se puede convertir en una multiplicación, y, además, descartando la posibilidad de que se trate de una integral inmediata, se utilizará el método de integración por partes, que consiste en aplicar esta fórmula:

Para poder memorizarla fácilmente, podemos usar la siguiente regla mnemotécnica: "Un día vi un valiente soldadito vestido de uniforme"

Debemos tener en cuenta que: 

1. Uno de los factores del integrando será u y el otro será dv.
2. Se calcula du derivando u y se calcula v integrando dv.
3. Se aplica la fórmula.

NOTA: Es crucial elegir bien a quién sustituimos por u y a quién sustituimos por dv, pues podríamos complicar mucho la integral. 

Por eso, en el caso 1, he elegido como u a x^2, porque su derivada es fácil de calcular y además hace que se baje un grado el exponente. Como vemos, después hay que aplicar de nuevo la integración por partes, pero después de ello no hay ningún problema en determinar la solución. A ser posible, sacamos factor común al final del ejercicio (lo suelen ver más "estético"). 

Realmente todos los casos que son por partes tienen un protocolo idéntico, pues debemos seguir la fórmula. Habrá veces en las que se necesite combinar la integración por sustitución con la integración por partes, y otras, como hemos podido comprobar, que necesitan más de una integración por partes. 

Otras veces, encontramos que la integral que teníamos en el enunciado, se repite, como por ejemplo ,en el caso 12. No debemos alarmarnos, simplemente le otorgaremos a la integral el valor de una incógnita, como por ejemplo, "I", y despejaremos como si fuera una ecuación normal. 

Es frecuente que la integración por partes se emplee en los siguientes casos(no quiere decir que sea infalible en estos casos o que no haya otros en los que se puedan aplicar, porque de hecho en las siguientes hojas hay varios casos que no coinciden con esto):

1. Polinomio por exponencial
2. Polinomio por coseno
3. Polinomio por seno
4. Exponencial por seno
5. Exponencial por coseno

Aquí tenemos algunos ejemplos de sustitución(mirar explicación en la entrada anterior):

Finalmente, un ejercicio que puede que nos pidan: Calcular la primitiva de una función. Para empezar, ¿qué es la primitiva de una función? Es la función a partir de la cual procede una función derivada. Es decir, si me dan la función f(x), me están dando la derivada y queremos encontrar la función de la que procede esta. (Mira la primera entrada de integrales, ahí se explica en el concepto de integral indefinida).
∫ f(x) dx = F(x) + C

Lo que buscamos es esa F(x).
Además, como me dicen que pasa por un punto en concreto, ya tenemos valores para x y para F(x) ( que es "y"). Así no hay posibilidad de infinitas primitivas, porque despejamos la constante K y ya sabemos cuál es.

INTEGRALES. SUSTITUCIÓN.

INTEGRALES POR SUSTITUCIÓN. 

Aquí tenemos a las integrales que más nos asustan. Es importante practicar todo lo que podamos, pues tenemos métodos para resolverlas que se suelen repetir con frecuencia. En esta entrada lo que haremos será analizar las integrales por sustitución más típicas, o que sirven de modelo para otras muy parecidas.

Antes de arriesgarnos a decir que estamos ante una integral que se resuelve por sustitución, tendremos que haber descartado todas las demás posibilidades. De no ser así, podríamos enredar mucho el problema. 

1. En el caso 3, la pista que nos indicará que puede tratarse de una sustitución es esa raíz con la x. En esta situación, x será sustituida por "t" elevado a aquel número que nos permita sacarla de la raíz. Como aquí tenemos una raíz cuadrada, será t^2. Es importante deshacer el cambio para dar la solución definitiva de la integral. 
2. En el caso 4, lo que igualaremos a t será e^x. Después de simplificar, vemos que es una racional. La resolvemos y finalmente deshacemos el cambio. 
3. El caso 5 es un poco distinto. Cuando encontramos razones trigonométricas, debemos tener muy presentes todas las fórmulas en relación que podamos. Comenzaremos desglosando lo que viene dentro de la integral, de manera que nos queda sen^2x*senx*cos^2x. Como tenemos senx, que es la derivada del cosx, será sen^2x quien sustituiremos por 1-cos^2x (de acuerdo a la igualdad sen^2x*cos^2x=1 ). A continuación, iremos multiplicando poco a poco lo que queda, y finalmente, por las propiedades de las integrales, separamos en dos integrales inmediatas. 

4. El caso 6 también es especial porque tenemos una fórmula en concreto para poder resolverlo; cuando tengamos sqrt(c-ax^2), sustituiremos x por x=sqrt(c/a)*sent. NOTA: Nunca olvidaremos que dx también tiene que ser sustituido, y para saber cuál es su valor, debemos, tras despejar "x", derivar, tanto en el lado de x como en el lado de t, despejando dx. En este tipo de integrales, debemos buscar la expresión sqrt(1-sen^2t). Por eso, sacamos de factor común el 3 y fuera de la integral sqrt3. 

5. Estos dos casos son realmente parecidos, y se pueden llevar a cabo por partes. (Ir a la siguiente entrada para entenderlo):

6. Aquí será relevante emplear las fórmulas del coseno del ángulo doble, así como la igualdad fundamental de la trigonometría (cos^2x+sen^2x=1). Sustituimos en la ecuación del coseno del ángulo doble, o bien el seno, o bien el coseno, porque en este caso ambos van a ser necesarios. Una vez hemos despejado, nos percatamos de que estamos ante una "suma por diferencia", por lo que se resolverá haciendo la suma de sus cuadrados. Como es una suma, por las propiedades de las integrales, se puede dividir en dos integrales distintas que se suman. De esta manera quedan como integrales inmediatas.

7. El caso 14 también requiere de fórmulas trigonométricas, y se aplicará aquella que aparece a continuación enmarcada en rojo, pues estamos multiplicando el coseno de un ángulo por el coseno de otro. Solo debemos seguir esa fórmula y, si sabemos hacer todo lo que se ha indicado hasta ahora, no habrá problemas en su resolución.

8. El caso 13 es prácticamente igual que el que he indicado en el punto 6. Sin embargo, aquí el senx está elevado a 4. Seguiremos el mismo protocolo. Sin embargo, aquí deberemos resolver el cuadrado que queda y además, quedará una suma más larga de integrales, pero el método es exactamente el mismo.

9. El caso 15 es igual que el 14, solo que esta vez es con senx. Seguiremos la fórmula marcada en rojo, separamos la integral en suma de integrales, y resolveremos estas, que son inmediatas.

10. Para nuestra sorpresa en el caso 16 encontramos una logarítmica, pues aunque a primera vista no se diferencie muy bien, si desarrollamos el seno de un ángulo doble, y hacemos la derivada del denominador, veremos que solo nos falta un -8 que podemos ajustar. (NOTA: Hay un error, en este ejercicio f(x)= 9-4cos^2x. Añadir ese 9-... no influye en el resultado, pero está mal decir que la función prescinde de esa parte, y queda contradictorio porque luego en el resultado sí ponemos ese 9-...).

10. El 17 es prácticamente igual que el primer caso que hemos hecho, y vemos con qué valor de "t" podríamos sacarla de la raíz. En caso de tener varias raíces, como está pasando ahora, haremos el mínimo común múltiplo entre todas ellas. Aquí será 4. Nos queda una integral racional que ya sabemos resolver. (Mira mi entrada "In. Racionales, arcotangentes, arcosenos" si no sabes resolverla).

11. Con las integrales como la que aparece en el caso 21 debemos de ser algo perspicaces. Muchas veces, pensamos que es una integral que se resuelve por sustitución y lo cierto es que podría ser una integral inmediata exponencial. Dan el mismo resultado, pero el tiempo que se emplea en una y en otra es muy valioso y útil para realizar otros ejercicios. Sin embargo, no podemos decir que este caso sea uno de ellos, pues si derivamos el denominador, lo que tendríamos que tener en el numerador sería 3^x*ln3*1, y tenemos ese 9^x que nos daría problemas. Es por eso que usaremos la táctica de la sustitución, y t=3^x. Si nos fijamos, la sustitución que hemos hecho es la misma que la que hicimos en el segundo caso, igualando a "t"directamente una parte de la integral. Esto también podrá suceder cuando tengamos: lnx, logax, arcsenx y arctgx.

12. De nuevo, en el caso 22, lo que haremos será igualar "t" a 5^x. Recordemos que el ln de un número, es una constante que se puede sacar de la integral, y que si tenemos t*(...), en realidad esa t es una (t+0) que funciona como una raíz. Como aquí lo que tenemos es t^2, en la primera división tendremos A/t, y en la segunda, B/t^2. Resolvemos como sabemos las racionales, y deshacemos el cambio. 

INTEGRALES. Racionales, arcotangente, arcoseno.

INTEGRALES RACIONALES. 

Debemos tener cuidado a la hora de pensar que estamos ante una integral racional, así como destacar la importancia de tenerlas en cuenta en todo momento (a mí, en concreto siempre se me olvidan que están ahí y pienso que es cualquier cosa menos una racional). 

En todo caso, si estamos pensando en que lo que estamos viendo es una integral racional, esta podrá aparecer de varias maneras:

1. El polinomio del numerador es de mayor o igual grado que el del denominador. En este caso, se deberán dividir ambos polinomios. Un ejemplo de ello lo podemos encontrar en los apartados c y h aquí adjuntos, en la segunda hoja. Como podemos observar, tras dividir numerador entre denominador, el resultado quedará como una suma de integrales: en la primera integral constará el cociente, y en la segunda el resto entre el dividendo. La integral que obtenemos del cociente suele ser de las más sencillas, por lo que su resultado se puede saber directamente. En el caso de "c" tenemos como cociente "1" y en "h" será "8x", siendo el resultado de su integración "x" y "(8x^2)/2", respectivamente. No obstante, en la otra integral que nos queda, resto entre dividendo, obtenemos un numerador de menor grado que el denominador.Aún así seguirá siendo racional, y se procederá de la misma manera que si en la integral del enunciado nos diesen un polinomio de menor grado dividido entre otro de mayor grado. 
2. Por esto, será la otra forma en la que puede aparecer una racional. Cuando el polinomio del denominador tiene un grado mayor que el del numerador, lo que haremos será factorizar este primero, de modo que la integral se pueda dividir en la suma de tantas integrales como resultados de x haya. Es decir, si tengo x=2 y x=-2 (ejemplo "b"), la integral se dividirá en la suma de 2 integrales, cada una con un resultado de x que se pondrá en el denominador. En los numeradores pondremos las incógnitas A,B,C,D, etc. Aquí es importante tener en cuenta varios factores: 

       - Si tenemos una raíz real simple (RRS), se procederá como se acaba de explicar. 

      -Sin embargo, si tenemos una raíz real múltiple (RRM) (ejemplo "a"), la integral será igual a la suma de tantas integrales como x haya, pero como se repite un número, en el caso presentado, el x=-3, la primera integral que aparezca como x+3 aparecerá elevada a 1, y la siguiente será (x+3)^2. Si tuviéramos un número que se repitiese tres veces, como por ejemplo el x=4, en la primera integral aparecería con su denominador como (x-4)^1, la segunda, (x-4)^2, y la tercera, (x-4)^3.

        - Por otro lado, también podemos encontrarnos con el caso de una raíz imaginaria, es decir, lo que hemos puesto siempre como "no existe", lo que haremos será, como en el caso "j", añadir ese polinomio sin descomponer. En esta situación tenemos (x^2)-4, por lo que al igualar la integral inicial a la suma de integrales, nos encontramos con que ese (x^2)-4 sigue intacto en el denominador, y además, en su numerador, añadiremos una x, teniendo Cx+D. 

Tras haber igualado la integral inicial a la suma de integrales, procederemos a hacer el mínimo común múltiplo entre esas sumas. De esta forma, el numerador de la primera integral quedará igualado a los numeradores de las sumas de integrales ajustados tras hacer el mínimo común múltiplo. Llegados a este punto, empezaremos a sustituir valores de "x" (a ser posible, los que anulen alguna de las raíces para poder despejar alguna de las incógnitas) y obtenemos los resultados de A, B, C, D... 

Ahora lo que haremos será irnos a nuestra integral inicial e igualarla de nuevo a esa suma de integrales, pero esta vez con todas las incógnitas encontradas. Se nos quedarán probablemente integrales logarítmicas o de tipo arcotangente, que veremos a continuación. 

DE TIPO ARCOTANGENTE. 

Las integrales de tipo arcotangente que podemos encontrar pueden venir camufladas de varias maneras. Están las que son más fáciles de ver, como las que presento en las siguientes tres primeras hojas. En ellas solo debemos ver que en el denominador queremos la expresión de (1+ algo^2), por lo que haremos los ajustes que sean necesarios para llegar a ello. En los ejercicios de la primera hoja ni siquiera hay que realizar dichos ajustes, pues ya prácticamente tenemos la forma que queremos. Pero muy pocas veces(y me atrevería a decir ninguna) nos pondrán en un examen algo así. Es fundamental que recordemos que todo aquello que queremos sacar de la integral sale TAL CUAL. Es decir, como en las de tipo arcotangente lo que solemos hacer es sacar factor común en el denominador para tener ese "1+..", saldrá fuera de la integral como denominador de una fracción. 

.

Sin embargo, aunque sigamos teniendo casos como estos en los apartados "v" y "x" (4º hoja), a primera vista nos pueden asustar un poco. Recordemos que cuanto más "fea" parezca una integral por fuera, resulta ser de las más fáciles. Y en efecto, al final nos damos cuenta de que tenemos en la propia integral la derivada de la secante (en v) y la derivada de la cosecante (en x). 

NOTA: Los asteriscos (o,t) en esta última hoja indican que no se pueden resolver, pues la variable x no coincide con la de la derivada de f(x).

Por otro lado, además, nos podemos cruzar con aquellas integrales que miramos y decimos "esta es racional" cuando en realidad hablamos de una arcotangente. Es el caso de los apartados "p", "q", y "r". En ellos, procederemos de la siguiente manera (mucha atención aquí):

1.  Multiplicamos numerador y denominador por "4*a" (Recordemos esta expresión: ax^2+bx+c)
2. El numerador lo sacamos fuera de la integral, y en el denominador, sin realizar las operaciones, iremos multiplicando esa expresión 4*a por cada uno de los componentes del polinomio. 
3. Ahora intentaremos "buscar el cuadrado". Recordemos que para que sea arcotangente necesitamos ese "algo" elevado al cuadrado, que será una suma. Todos conocemos (o al menos deberíamos conocer) lo de "Suma de binomios es igual al cuadrado del primero más el cuadrado del segundo más el doble del primero por el segundo".  
4. Buscando el cuadrado: Del primer sumando de lo que queda tras multiplicar 4*a por el polinomio extraemos sus cuadrados, es decir, si tenemos 4x^2, sacamos 2x. Ese será nuestro primer componente de la suma al cuadrado. Lo sumamos a una incógnita "b", con lo que queda como "(2x+b)^2. Para hallar "b", pasaremos al siguiente sumando, en el cual tendremos que encontrar la expresión "más el doble del primero por el segundo", es decir, con el ejemplo dado, tendremos que encontrar 2*2*x*b. Como vemos en "p", tenemos 4*10*x, establecemos la siguiente relación : 2*2=4, x=x, y, por tanto, b=10. En el caso de que no encontremos b de manera explícita, será igual a 1. Además, ahora lo que tendremos que hacer será seguir con ese cuadrado, por lo que nos falta "el cuadrado del segundo", es decir, el cuadrado del número que hemos obtenido. Como es algo que "nos inventamos", algo que no estaba en la integral y lo añadimos nosotros porque es necesario, y es un sumando, pondremos al lado el mismo valor restando. Osea, si b=10, pondremos al lado +100 -100. El +100 pertenece al cuadrado de la suma que estábamos buscando, pero, ¿y el -100?: El -100 se juntará con el resultado que dé ese tercer sumando que se obtenía cuando multiplicábamos 4*a por el polinomio. ATENCIÓN: El resultado de ese -100 con lo dicho deberá ser un número positivo.
5. Ya tendríamos una forma de arcotangente que sí sabríamos resolver sacando factor común y haciendo el mismo proceso que se ha explicado antes.

DE TIPO ARCOSENO. 

Las integrales de tipo arcoseno tienen un procedimiento muy similar a las de tipo arcotangente, pero en este caso buscaremos en el denominador la expresión de "sqrt(1-algo^2)". Es por esto que cuando queremos sacar factor común, sale fuera de la integral como denominador en forma de raíz de una fracción. De nuevo, podemos hallar tanto casos sencillos como aquellos en los que solo debemos sacar factor y elevar al cuadrado lo que va después del "1-...", como casos en los que debemos buscar el cuadrado. Hablemos de estos últimos. 

A veces encontramos el polinomio completo, como es en el apartado "e". Para resolverlo, dejaremos "c" (ax^2 + bx+c) fuera de ese paréntesis que nos servirá para poner ahora "el cuadrado de la resta de binomios". Así, el 9 queda fuera con un - tras de él para que "a" se quede positiva y tengamos (ax-b)^2. Multiplicamos numerador  denominador por sqrt(4*|a|). Cuando hayamos hecho todo eso, buscamos el cuadrado (ver arriba cómo se hace, es de la misma manera), y ya solo quedaría sacar factor común y ajustar el cuadrado con el número que hemos sacado de factor común introducido en la expresión. 

Otras veces, no obstante, no tenemos el polinomio completo, sino que tenemos en el denominador, por ejemplo, sqrt(x-5x^2). No debemos asustarnos, el procedimiento será el mismo, solo que cuando saquemos el - para tener el x^2 positivo, no habrá ningún número delante, pero al final quedará ese "cuadrado del segundo" que deberemos introducir para poder completar esa resta al cuadrado. 

PD: Estos ejercicios los hice cuando estaba estudiando para el primer parcial en el que nos examinamos de integrales, y corrigiéndolos ahora me he dado cuenta de muchos fallos, por lo que están prácticamente todos pasados por mi vista actual. Sin embargo, sé que puede haber aún un montón de fallos así que si alguien encuentra alguno no me sorprendería

INTEGRALES. Potenciales,logarítmicas,exponenciales.

                                                                                             

¡Y vamos con las integrales! Iré poniendo primero las más fáciles, las "inmediatas", y poco a poco se subirá la dificultad. 

Pero antes de nada, ¿qué es una integral? 

La integral definida es un concepto utilizado para determinar el valor de las áreas limitadas por curvas y rectas. Dado el intervalo [a, b] en el que, para cada uno de sus puntos x, se define una función f(x) que es mayor o igual que 0 en [a,b], la integral definida de la función entre los puntos a y b es el área de la porción del plano que está delimitada por: la función, el eje horizontal OX y las rectas verticales de ecuaciones x=a y x=b.
Sin embargo, la integral indefinida, de la cual vamos a ver multitud de ejemplos a continuación, es el conjunto de infinitas primitivas que puede tener una función, y se representa por: ∫ f(x) dx y su resultado da: F(x) + C. 

Además, cabe determinar que una integral permite restituir una función que ha sido previamente derivada. Por ello, si al calcular una integral quisiéramos comprobar que la hemos realizado correctamente, bastaría con derivar el resultado obtenido y verificar que sea el mismo que la integral que nos dan en el enunciado. 

Así pues, pasemos a operar. A continuación, las integrales inmediatas de tipo "Potencial", "logarítmico" y "exponencial". 

DE TIPO POTENCIAL. 

Como podemos ver en la formula que aparece en la parte superior del folio, en las integrales de tipo potencial simple tan solo habrá que elevar a un número más (n+1) a la variable x.

Las números que aparecen acompañando a dicha variable (como, por ejemplo, en el apartado b) se sacan y ocupan el mismo lugar que ocupaban dentro de la integral (es decir, si es una fracción, se saca tal cual). Sin embargo, a la hora de que tengamos que introducir nosotros una constante, esta se manifestará fuera de la integral como su inversa (es decir, si quiero meter un 8 dentro de la integral, fuera quedará como 1/8).

La integral potencial compuesta no difiere demasiado. En ella, lo único distinto que encontramos es que es una función la que está elevada a algo, mientras que en las simples solo era la x la que estaba elevada. En las compuestas lo primero que debemos hacer es localizar f(x), y esto lo conseguiremos observando primero cuál es la función que está elevada a algún número, seguido de la comprobación de que tenemos multiplicando a dicha función f(x) su derivada. Solo habrá que introducir constantes, pues bajo ningún concepto se podrán añadir variables.

INTEGRALES DE TIPO LOGARÍTMICO. 

Estas integrales son sencillas de ver, pues en el denominador encontramos f(x) y en el numerador su derivada. Sin embargo, muchas veces puede venir camuflada, de formas que hagan que nos confundamos o que no sepamos qué hacer, como en el ejemplo "g". En este ejemplo, en concreto, al igual que hemos hecho en el "n", al ver ese actgx o arcsenx, ya sabemos que la derivada de ellos debe ser una fracción, por lo que colocaremos la integral de manera que el denominador sea la función que arriba tenga su derivada. 

NOTA: A veces, las potenciales y las logarítmicas, a simple vista, se pueden confundir. Esto es porque podemos encontrar una integral que tenga en el denominador una raíz y en el numerador su derivada. No nos dejemos engañar. La función raíz sube al numerador con un signo "-"  con lo que se evidenciará que se trata de una potencial, no una logarítmica. Ahora sería normal preguntarse "¿entonces, por qué no puedo hacer lo mismo con todas las que parecen logarítmicas? La respuesta es sencilla, si subimos una función que está elevada a 1, quedaría como -1, y de acuerdo a la regla de las potenciales, a "n", que sería -1, habría que sumarle 1, por lo que el resultado sería 0 y no nos daría el verdadero resultado de la integral. 

INTEGRALES DE TIPO EXPONENCIAL. 

Las integrales de tipo exponencial son las más fáciles de identificar, ya que tenemos, o bien "e" elevado a una función, o un número elevado a una función. 

En el primer caso, solo habrá que localizar esa función que acompaña a "e " y la correspondiente derivada de dicha función, introduciendo o sacando constantes según se dé el caso. El resultado será esa misma "e^f(X)" junto con la variación de constantes y +K.

En el segundo caso, el de un número (base) elevado a una función, además de ajustar las constantes, también se tendrá que buscar el ln de la base. 

BIBLIOGRAFÍA. (definición de integral)
http://www.hiru.eus/es/matematicas/la-integral-definida

AN. Ej6. FUNCIONES II. Valor absoluto.

Esta función cuenta de nuevo con un valor absoluto, así que consideraremos tanto la opción de que x sea un número positivo, como de que sea uno negativo. Recordemos que podemos cambiar el signo del numerador o del denominador en caso de que x sea menor que 0. Si x es un número mayor o igual que 0, no habrá necesidad de cambiar el signo. 

En ambas partes, por dominio, podríamos determinar que x=2 sería un problema. Sin embargo, no cumple la primera condición de x<0, pero sí cumple la segunda, pues 2>/=0.

Estudiamos entonces la función para x=2 y x=0, esta última por salto de función. Vemos que, como para x=2, va a más y menos infinito, hay una asíntota vertical. Comprobación del límite por Symbolab: 

 (Sé que la imagen es muy pequeña, pero he tratado de recortarla varias veces con el ordenador para ampliarla y se me ha hecho imposible).

Comprobaremos después si hay asíntotas horizontales, haciendo el límite, tanto para x->+ infinity como para x-> -infinity. Como es una función a trozos, cuando x tiende a menos infinito, haremos el límite del trozo cuya condición es que x sea menor que 0. Cuando x tiende a más infinito, haremos el límite del que cumple la condición de que x>/=0. En ambos casos se obtiene un resultado, teniendo una asíntota horizontal por la izquierda para y=-1 y una asíntota horizontal por la derecha en y=1. 

Finalmente, estudiaremos la monotonía, haciendo la primera derivada de la función, y dibujándonos al lado la recta real con los intervalos a estudiar. 

Un punto del primer intervalo, que va desde -infinity hasta 0, se sustituirá en la primera derivada del primer trozo de esta función, consiguiendo un signo positivo, por lo que crece. 

En cambio, los puntos de los intervalos que van desde 0 a 2 y de 2 a +infinity, serán sustituidos en la primera derivada del segundo trozo de la función, es decir, la que está definida para números mayores o iguales a 0. Para ambos casos la función decrece, habiendo un máximo relativo en x=0. 

Representación gráfica mediante Geogebra:

AN.Ej5. FUNCIONES I.

 La función que se nos presenta es una muy sencilla de tipo polinómica, cuyo dominio serán todos los números de la recta real, por ello será continua, y no tendrá asíntotas verticales. Tampoco las habrá horizontales porque deberíamos hacer el límite de esa función cuando tiende a infinito, y el resultado nos daría también infinito. 

Estudiamos la monotonía, haciendo la primera derivada de la función. Despejando x, obtendremos los valores que serán posibles candidatos para ser máximos y mínimos. Realizamos una tabla con los intervalos que proporcionan los puntos sacados de esa primera derivada, y sustituimos valores que se encuentren entre dichos intervalos.Si el signo que sale de sustituir un punto de ese intervalo en la primera derivada de la función, es positivo, quiere decir que la función está creciendo. Si sale negativo, es que decrece. Como se ve aquí, crece en el intervalo de (-infinity, 0], y  en el de (2,+infinity), mientras que decrece en el de (0,2]. Con esta tabla ya podríamos saber si disponemos de máximos y mínimos, pero conviene formalizarlo y escribirlo en forma de segunda derivada, sustituyendo en ella aquellos candidatos que se han mencionado antes. Si el resultado obtenido es menor que 0, significa que en ese punto habrá un máximo, y si el resultado es mayor que 0, significará que hay un mínimo.  

Una representación gráfica con Geogebra: 

AN. EJ4. CONTINUIDAD Y VALOR ABSOLUTO II.

En este ejercicio, se nos pide hallar el valor de los parámetros a y b para que la función dada sea continua para todos los números de la recta real. 

Lo que llama la atención de esta función es que en las condiciones hay valores absolutos. Como se ha indicado en otro ejercicio de análisis, debemos considerar, por un lado, que x sea positiva, que según al primera inecuación (encuadrada de rojo) dará un número menos o igual que 3. En cambio, si x fuera un número negativo menor o igual que 3, buscaremos convertir a x en un valor positivo, por tanto, según las reglas de las inecuaciones, para cambiar el signo de x y el de -3, debemos cambiar asimismo el sentido de la inecuación. Nos queda x>/= -3. Si representamos estos valores en la recta real, veremos que hay un intervalo que coincide en ambas condiciones, así que podemos condensarlo de la siguiente manera: -3</=x</=3. 

En el recuadro verde procederemos de la misma forma, de modo que si x es un valor positivo, se quedará como x>3. En cambio, cuando x es un valor negativo, -x>3, cambiamos el signo de x para que sea positivo, haciendo variar también el de 3 y cambiando el sentido de la inecuación, x<-3. Si representamos ambos intervalos en la recta real, no podemos encontrar una parte común, así que se quedan como están.

Lo siguiente que haremos será "ordenar" la función. Hemos obtenido las siguientes condiciones: si -3</=x</=3, si x<3, y si x<-3. Las ordenamos como irían en la recta real quedando como se muesra en el ejercicio. 

Los puntos a estudiar para la continuidad, según el salto de función, serían -3, y 3. Sin embargo, en aquellos sitios e los que haya una fracción, también se debería considerar el 0, pero como donde hay fracciones las condiciones dadas no incluyen el 0, no hace falta estudiarlo. 

Hacemos f(-3) y sus límites laterales, y, además, como la condición del ejercicio es que sea continua, igualaremos f(-3) a los límites laterales. 

Haremos lo mismo para x=3, y hacemos un sistema de ecuaciones que nos permite sacar los parámetros. 

AN.Ej3. CONTINUIDAD.

En este ejercicio haremos un estudio de la continuidad. Una función es continua si su gráfica puede dibujarse de un solo trazo. 

Como estamos ante una función racional, su continuidad vendrá determinada por el Dominio. Vemos así para qué valores de x se anula el denominador, y estudiamos la función en cada uno de esos puntos y sus límites laterales. 

Para x=0, f(0) no existe al sustituir el valor en la función, mientras que los límites laterales, como es una indeterminación 0/0 y podemos factorizar y simplificar obtenemos, en ambos casos, -1/2. Se trata de una discontinuidad evitable. 

En el caso de x=1, pasa lo mismo. 

Sin embargo, para x=2 lo que tenemos es que los límites laterales van hacia +infinity y -infinity, por lo que tendremos, para ese valor, una asíntota vertical. 

Gracias al programa de Geogebra podemos representar la función, en la que se distingue claramente la asíntota vertical en x=2. 

AN.Ej2. VALOR ABSOLUTO EN UN LÍMITE.

Cuando encontremos un valor absoluto, lo primero que debemos hacer es comprobar para qué valor aquello que está dentro nos daría un número negativo, porque precisamente la condición de valor absoluto implica que el resultado que se obtenga, sea el número que sea, dé positivo. Como este límite es de tipo k/0 y para resolverse debemos estudiar los límites laterales, cuando 2 viene por la izquierda quiere decir que es un número un poco más pequeño que 2, es decir, 1.9. Si sustituimos el valor de 1.9 en las barras de valor absoluto, se puede ver que dará un número menor que 0, (1.9-2=-01). Como da un resultado negativo y no queremos eso, cambiaremos el signo o bien del numerador, o bien del denominador. En este caso he cambiado el del denominador. De esta forma, el valor de 2-x para cuando 2 tiende hacia la izquierda, dará un resultado positivo, tal y como se buscaba. 

Cuando 2 tiende hacia la derecha, cogeremos un número algo mayor que 2, como 2.1. Debido a que al sustituir 2.1 en el valor de x del valor absoluto obtenemos un número positivo, no tendremos que cambiar ningún signo.  

CÁLCULO DE UN LÍMITE.

 Empezamos con el bloque de Análisis.
A continuación, haremos el siguiente límite:

Como se puede observar, al sustituir el valor de x =1 en el límite, obtenemos un tipo de indeterminación: 0/0. Las dos maneras prototípicas de resolver este tipo de límites, son dos: 

1. Factorizando numerador y denominador y simplificando. 

2. Aplicando L-Hôpital; que consiste en derivar tanto el numerador como el denominador, pero no como un cociente, sino cada uno por su lado. 

Llevando a cabo la forma 2, derivamos, por un lado el numerador, siendo la derivada de una constante, 0, y la derivada del coseno, -sen (como está multiplicado a una constante esta se deja tal cual). Por otra parte, derivamos el denominador, que, al ser una raíz cuadrada pondremos como potencia para que, al derivar, el exponente multiplique a la base y se le reste 1 unidad a su valor. 

Comprobamos los resultados con el programa Mathics, aunque también podemos emplear Wolframalpha o Symbolab.