INTEGRALES. POR PARTES.

EJERCICIOS DE INTEGRACIÓN POR PARTES. 

Cuando vemos que el integrando está formado por un producto, o por una división que se puede convertir en una multiplicación, y, además, descartando la posibilidad de que se trate de una integral inmediata, se utilizará el método de integración por partes, que consiste en aplicar esta fórmula:

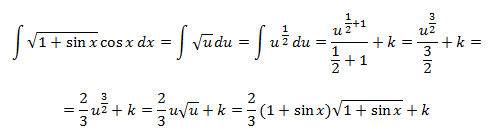
Para poder memorizarla fácilmente, podemos usar la siguiente regla mnemotécnica: "Un día vi un valiente soldadito vestido de uniforme"

Debemos tener en cuenta que: 

1. Uno de los factores del integrando será u y el otro será dv.
2. Se calcula du derivando u y se calcula v integrando dv.
3. Se aplica la fórmula.

NOTA: Es crucial elegir bien a quién sustituimos por u y a quién sustituimos por dv, pues podríamos complicar mucho la integral. 

Por eso, en el caso 1, he elegido como u a x^2, porque su derivada es fácil de calcular y además hace que se baje un grado el exponente. Como vemos, después hay que aplicar de nuevo la integración por partes, pero después de ello no hay ningún problema en determinar la solución. A ser posible, sacamos factor común al final del ejercicio (lo suelen ver más "estético"). 

Realmente todos los casos que son por partes tienen un protocolo idéntico, pues debemos seguir la fórmula. Habrá veces en las que se necesite combinar la integración por sustitución con la integración por partes, y otras, como hemos podido comprobar, que necesitan más de una integración por partes. 

Otras veces, encontramos que la integral que teníamos en el enunciado, se repite, como por ejemplo ,en el caso 12. No debemos alarmarnos, simplemente le otorgaremos a la integral el valor de una incógnita, como por ejemplo, "I", y despejaremos como si fuera una ecuación normal. 

Es frecuente que la integración por partes se emplee en los siguientes casos(no quiere decir que sea infalible en estos casos o que no haya otros en los que se puedan aplicar, porque de hecho en las siguientes hojas hay varios casos que no coinciden con esto):

1. Polinomio por exponencial
2. Polinomio por coseno
3. Polinomio por seno
4. Exponencial por seno
5. Exponencial por coseno

Aquí tenemos algunos ejemplos de sustitución(mirar explicación en la entrada anterior):

Finalmente, un ejercicio que puede que nos pidan: Calcular la primitiva de una función. Para empezar, ¿qué es la primitiva de una función? Es la función a partir de la cual procede una función derivada. Es decir, si me dan la función f(x), me están dando la derivada y queremos encontrar la función de la que procede esta. (Mira la primera entrada de integrales, ahí se explica en el concepto de integral indefinida).
∫ f(x) dx = F(x) + C

Lo que buscamos es esa F(x).
Además, como me dicen que pasa por un punto en concreto, ya tenemos valores para x y para F(x) ( que es "y"). Así no hay posibilidad de infinitas primitivas, porque despejamos la constante K y ya sabemos cuál es.